5 Creating Maps
When I first started learning R, I considered it a tool for working with numbers, not shapes, so I was surprised when I saw people using it to make maps. Abdoul Madjid, a developer, has been creating maps with R for several years. Recently, he used one to visualize rates of COVID-19 in the United States in 2021.
You might think you need specialized mapmaking software like ArcGIS to make maps, but this tool is expensive, and while Excel has added support for map-making in recent years, its features are limited (for example, you can’t use it to make maps based on street addresses). Even QGIS, an open source tool similar to ArcGIS, still requires learning new skills.
Using R for map-making has benefits. It lets you perform all of your data manipulation tasks with one tool and apply the principles of high-quality data visualization discussed in Chapter 3. For example, Madjid used R to obtain his data, analyze it, and make his COVID-19 map, which you can see in Figure 5.1.
Figure 5.1: Abdoul Madjid’s map of COVID in the United States in 2021
In this chapter, we’ll explore principles of working with geospatial data, then walk through Madjid’s code to understand how he created this high-quality map. We’ll also discuss where to find geospatial data and how to use it to make your own maps.
The Briefest of Primers on Geospatial Data
You don’t need to be a GIS expert to make maps. But you do need to understand a few things about how geospatial data works, starting with its two main types: vector and raster. Vector data uses points, lines, and polygons to represent the world. Raster data, which often comes from digital photographs, ties each pixel in an image to a specific geographic location. Vector data tends to be easier to work with, and we’ll be using it exclusively in this chapter.
In the past, working with geospatial data meant mastering competing standards, each of which required learning a different approach. Today, though, most people use the simple features model for working with vector geospatial data (often abbreviated as sf), which is way easier to understand. For example, take a look at some simple features geospatial data that represents the US state of Wyoming:
You can see that the data has two columns, one for the state name (NAME) and another called geometry. This data looks like the data frames you’re used to encountering, aside from two major differences: There’s a bunch of metadata above the data frame, and our simple features data contains geographical data in a variable called geometry. The metadata begins with the text “Simple feature collection with 1 feature and 1 field” (because the geometry column must be present in order for a data frame to be geospatial data it is not counted as a field). The feature referenced here is the row, and the field is the NAME variable, which contains non-spatial data (the geometry column will be discussed below). This line, and the lines that follow, are metadata about the geospatial data in the wyoming object. Let’s look at each part of this simple features data.
Geometry Type
The geometry type represents the shape of the geospatial data we’re working with. These types are typically written in all caps. In this case, the relatively simple POLYGON type represents a single polygon. We can use ggplot to display this data by calling geom_sf(), a special geom designed to work with simple features data:
wyoming <- read_sf("https://data.rwithoutstatistics.com/wyoming.geojson")
wyoming %>%
ggplot() +
geom_sf()Figure 5.2 shows the resulting map of Wyoming. It may not look like much, but, hey, I wasn’t the one who chose to make Wyoming a nearly perfect rectangle!
Figure 5.2: A map of Wyoming
POLYGON is one of several geometry types that sf data can be used to represent.
Other geometry types used in simple feature data include POINT, to display elements such as a pin on a map that represents a single location. Figure 5.3 is a map showing the location of a single electric vehicle charging station in Wyoming.
Figure 5.3: A map of a single electric vehicle charging station in Wyoming
The LINESTRING geometry type is for set of points that can be connected with lines, often used to represent roads. The LINESTRING in Figure 5.4 shows a section of US Highway 30 that runs through Wyoming.
Figure 5.4: A map of a section of U.S. Highway 30 running through Wyoming
Each of these geometry types has a MULTI variation (MULTIPOINT, MULTILINESTRING, and MULTIPOLYGON) that combines multiple instances of the type in one row of data. For example, the data used to make Figure 5.5, which shows all electric vehicle charging stations in Wyoming, is MULTIPOINT.
Figure 5.5: A map of all electric vehicle charging stations in Wyoming
Likewise, we can use MULTILINESTRING data to show not just one road, but all major roads in Wyoming, as in Figure 5.6.
Figure 5.6: A map of all major roads in Wyoming
Lastly, we could use MULTIPOLYGON data to, for example, depict a state made up of multiple polygons. To see what I mean, take a look at a map of Wyoming’s counties. We can import this data with the following code:
The following simple features data represents the 23 counties in the state:
#> Simple feature collection with 23 features and 1 field
#> Geometry type: MULTIPOLYGON
#> Dimension: XY
#> Bounding box: xmin: -111.0546 ymin: 40.99477 xmax: -104.0522 ymax: 45.00582
#> Geodetic CRS: WGS 84
#> # A tibble: 23 × 2
#> NAME geometry
#> <chr> <MULTIPOLYGON [°]>
#> 1 Lincoln (((-110.54 42.287, -110.54 42.286, -110.54 4…
#> 2 Fremont (((-109.33 42.869, -109.33 42.869, -109.33 4…
#> 3 Uinta (((-110.58 41.579, -110.58 41.579, -110.58 4…
#> 4 Big Horn (((-107.5 44.64, -107.5 44.64, -107.5 44.641…
#> 5 Hot Springs (((-108.16 43.471, -108.16 43.46, -108.16 43…
#> 6 Washakie (((-107.68 44.166, -107.68 44.166, -107.68 4…
#> 7 Converse (((-105.92 43.495, -105.92 43.495, -105.91 4…
#> 8 Sweetwater (((-109.57 40.998, -109.57 40.998, -109.57 4…
#> 9 Crook (((-104.46 44.181, -104.46 44.181, -104.46 4…
#> 10 Carbon (((-106.32 41.383, -106.32 41.382, -106.32 4…
#> # ℹ 13 more rowsWe can see that the geometry type of this data is MULTIPOLYGON. In addition, the repeated MULTIPOLYGON text in the geometry column indicates that each row contains a shape of type MULTIPOLYGON. Figure 5.7 is a map made with this data.
Figure 5.7: A map of Wyoming counties
You can easily see the multiple polygons that make up the map.
The Dimensions
Next, the geospatial data frame contains the data’s dimensions, or the type of geospatial data we’re working with. In the Wyoming example, it looks like this: Dimension: XY, meaning the data is two-dimensional, as in the case of all the geospatial data used in this chapter. There are two other dimensions (Z and M) that you’ll see much more rarely. I’ll leave them for you to investigate further.
Bounding Box
The penultimate element in the metadata is the bounding box. A bounding box represents the smallest area in which we can fit all of our geospatial data. For our wyoming object, it looks like this:
Bounding box: xmin: -111.0569 ymin: 40.99475 xmax: -104.0522 ymax: 45.0059
The ymin value of 40.99475 and ymax value of 45.0059 represent the lowest and highest latitude, respectively, that the state’s polygon can fit into. The x values do the same for the longitude. Bounding boxes are calculated automatically, and you don’t typically have to worry about altering them.
The Geodetic CRS
The last piece of metadata specifies the coordinate reference system used to project our data when we plot it. The problem with representing any geospatial data is that we’re displaying information about the three-dimensional Earth on a two-dimensional map. Doing so requires us to choose a coordinate reference system that determines what type of correspondence, or projection, to use when making our map.
The data for the Wyoming counties map includes the line Geodetic CRS: WGS 84, indicating the use of a coordinate reference system known as WGS84. To see a different projection, check out the same map using what’s known as the Albers equal-area conic convenience projection. While Wyoming looked perfectly horizontal in Figure 5.7, the version in Figure 5.8 appears to be tilted.
Figure 5.8: A map of Wyoming counties using the WGS84 projection
If you’re curious about how to change projections when making maps of your own, fear not. You’ll see how to do this when we look at Abdoul Madjid’s map. And if you want to know how to choose appropriate projections for your maps, check out the conclusion of the chapter.
The geometry Column
In addition to the metadata, our simple features data differs from traditional data frames in another respect: its geometry column. As you probably guessed from the name, it holds the data needed to make our maps.
To understand how this works, consider the connect-the-dots drawings you probably completed as a kid. As you added lines to connect one point to the next, the subject of your drawing became clear. The geometry column is similar. It has a set of numbers, each of which corresponds to a point. If you’re using LINESTRING/MULTILINESTRING or POLYGON/MULTIPOLYGON simple features data, ggplot uses the numbers in the geometry column to draw each point and then adds lines to connect the points. If you’re using POINT/MULTIPOINT data, it draws the points but doesn’t connect them.
Once again, you never have to worry about these details or look in any depth at the geometry column.
Recreating the COVID Map
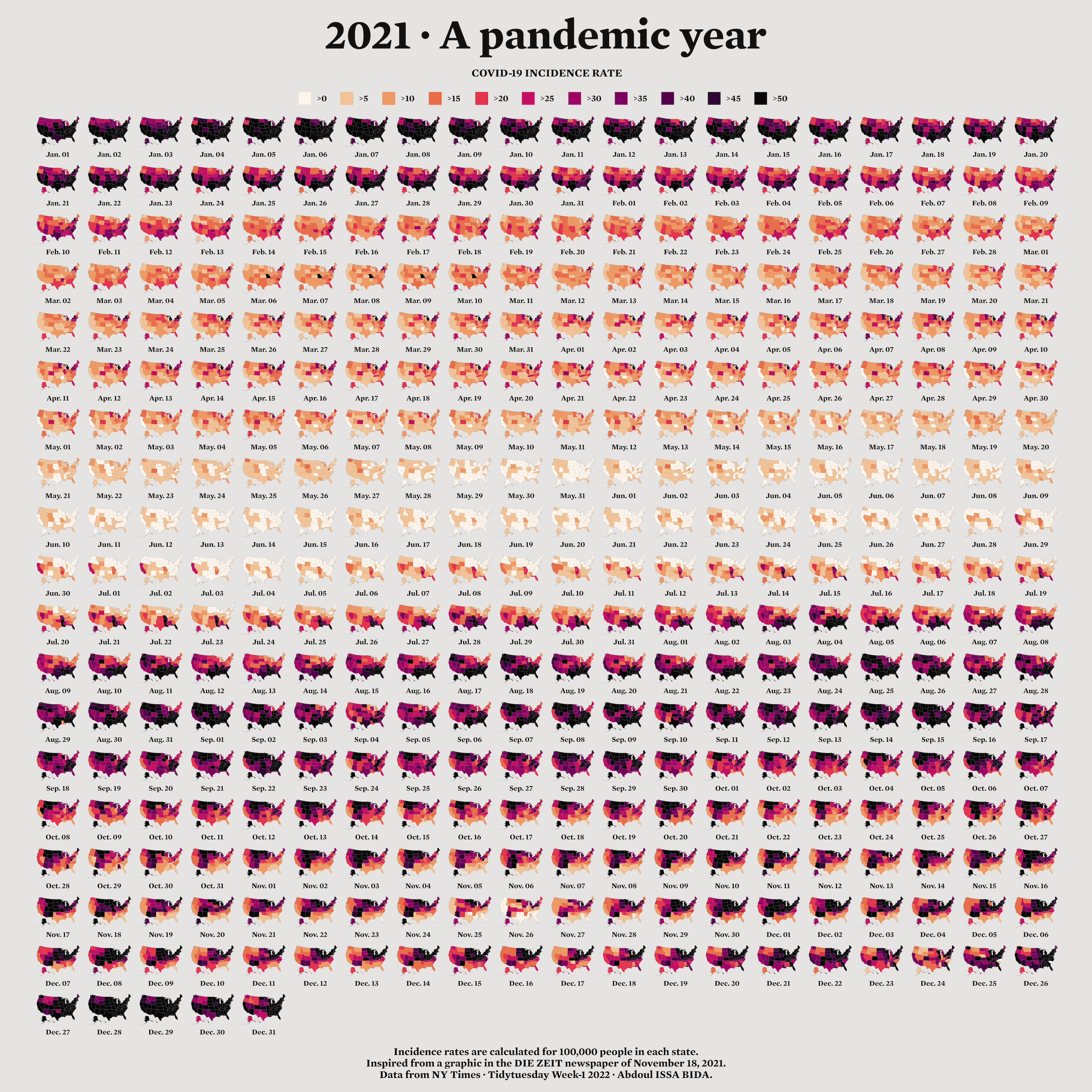
Now that you understand the basics of geospatial data, let’s walk through the code Madjid used to make his COVID-19 map., which makes use of the geometry types, dimensions, bounding boxes, projections, and the geometry column we just explored. (I’ve made some small modifications to the code to make the final map fit on the page.) Let’s begin by loading few packages:
We’ll use tidyverse to import data, manipulate it, and plot it (with ggplot). The albersusa package will give us access to geospatial data, and the sf package will enable us to change its coordinate reference system to use an appropriate projection. The zoo package has functions for calculating rolling averages, and the colorspace package gives us a color scale that highlights the data well.
Importing the Data
Next, let’s import the data we need. We require three pieces of data: COVID rates by state over time, state populations, and geospatial information. Madjid imported each of these pieces of data separately and then merged them, and we’ll do the same.
First, we import COVID data. This data comes directly from The New York Times, which publishes daily case rates by state as a CSV file on its GitHub account. I’ve dropped the fips variable; Federal Information Processing Standards (FIPS) are numeric codes used to represent states, but we can reference states by their names instead:
If you take a look at this data, you can see the arrival of the first COVID cases in the United States in January 2020.
#> # A tibble: 61,102 × 4
#> date state cases deaths
#> <date> <chr> <dbl> <dbl>
#> 1 2020-01-21 Washington 1 0
#> 2 2020-01-22 Washington 1 0
#> 3 2020-01-23 Washington 1 0
#> 4 2020-01-24 Illinois 1 0
#> 5 2020-01-24 Washington 1 0
#> 6 2020-01-25 California 1 0
#> 7 2020-01-25 Illinois 1 0
#> 8 2020-01-25 Washington 1 0
#> 9 2020-01-26 Arizona 1 0
#> 10 2020-01-26 California 2 0
#> # ℹ 61,092 more rowsMadjid’s map shows per capita rates (rates per 100,000 people) rather than absolute rates (the rates without consideration for a state’s population). So, to recreate his maps, we need to obtain data on each state’s population. Madjid downloaded this data as a CSV:
usa_states <- read_csv("https://data.rwithoutstatistics.com/population-by-state.csv") %>%
select(State, Pop)We import this data, keep the State and Pop (population) variables, and save it as an object called usa_states. Let’s see what usa_states looks like:
#> # A tibble: 52 × 2
#> State Pop
#> <chr> <dbl>
#> 1 California 39613493
#> 2 Texas 29730311
#> 3 Florida 21944577
#> 4 New York 19299981
#> 5 Pennsylvania 12804123
#> 6 Illinois 12569321
#> 7 Ohio 11714618
#> 8 Georgia 10830007
#> 9 North Carolina 10701022
#> 10 Michigan 9992427
#> # ℹ 42 more rowsFinally, we’ll bring in our geospatial data and save it as an object called usa_states_geom:
usa_states_geom <- usa_sf() %>%
select(name) %>%
st_transform(us_laea_proj)The usa_sf() function from the albersusa package gives us simple features data for all US states (and, conveniently, places Alaska and Hawaii in locations, and at a scale, that make them easy to see). This data includes multiple variables, but we need only the state names, so we keep the name variable only.
We then used the st_transform() function from the sf package to change the coordinate reference system. The one used here comes from the us_laea_proj object, from the albersusa package. Remember the Albers equal-area conic convenience projection we used to change the appearance of our Wyoming counties map? This is the same projection.
Calculating Daily COVID Cases
Next, we need to calculate the number of daily COVID cases. We have to do this because the covid_data data frame gives us cumulative cases by state, but not the number of cases per day:
covid_cases <- covid_data %>%
group_by(state) %>%
mutate(
pd_cases = lag(cases)
) %>%
replace_na(list(pd_cases = 0)) %>%
mutate(
daily_cases = case_when(
cases > pd_cases ~ cases - pd_cases,
TRUE ~ 0
)
) %>%
ungroup() %>%
arrange(state, date)We use the group_by() function to calculate totals for each state, then create a new variable called pd_cases, which represents the number of cases in the previous day (we can use the lag() function to assign data to this variable). Some days do not have cases counts for the previous day, so in these cases, we set the value to 0 using the replace_na() function. Finally, we create a new variable called daily_cases. To set the value of this variable, we use the case_when() function to set up a condition: if the cases variable (which holds the cases on that day) is greater than the pd_cases variable (which holds cases from one day prior), then daily_cases is equal to cases minus pd_cases; otherwise, we set daily_cases to be equal to 0. Because we grouped the data by state at the beginning, we must now remove this grouping using the ungroup() function before arranging our data by state and date. Now take a look at the covid_cases data frame we created:
#> # A tibble: 61,102 × 6
#> date state cases deaths pd_cases daily_cases
#> <date> <chr> <dbl> <dbl> <dbl> <dbl>
#> 1 2020-03-13 Alabama 6 0 0 6
#> 2 2020-03-14 Alabama 12 0 6 6
#> 3 2020-03-15 Alabama 23 0 12 11
#> 4 2020-03-16 Alabama 29 0 23 6
#> 5 2020-03-17 Alabama 39 0 29 10
#> 6 2020-03-18 Alabama 51 0 39 12
#> 7 2020-03-19 Alabama 78 0 51 27
#> 8 2020-03-20 Alabama 106 0 78 28
#> 9 2020-03-21 Alabama 131 0 106 25
#> 10 2020-03-22 Alabama 157 0 131 26
#> # ℹ 61,092 more rowsIn the next step, we’ll make use of the daily_cases variable.
Calculating Incidence Rates
We’re not quite done calculating values. The data that Madjid used to make his map didn’t include daily case counts. Instead, it contained a five-day rolling average of cases per 100,000 people. A rolling average is the average case rate in a certain time period. Quirks of reporting (for example, not reporting on weekends but instead rolling Saturday and Sunday cases into Monday) can make the value for any single day less reliable. Using a rolling average smooths things out. Here is the code to generate this data:
We create a new data frame called covid_cases_rm (where rm stands for rolling mean). The first step in its creation is to use the rollmean() function from the zoo package to create a roll_cases variable, which holds the average number of cases in the five-day period surrounding a single date. The k argument is the number of days for which we want to calculate the rolling average (five, in our case), and the fill argument determines what happens in cases like the first day, where we can’t calculate a five-day rolling mean because there are no days prior to this day (Madjid set these values to be NA).
After calculating roll_cases, we need to calculate per capita case rates. To do this, we needed population data, so we join the population data from the usa_states data frame with the covid_cases data:
We then drop rows with missing population data (the Pop variable). In practice, this means getting rid of several US territories (American Samoa, Guam, Northern Marianas Islands, and Virgin Islands).
Next, we created a per capita case rate variable called incidence_rate by multiplying the roll_cases variable by 100,000 and then dividing it by the population of each state:
mutate(incidence_rate = 10^5 * roll_cases / Pop) %>%
mutate(incidence_rate = cut(incidence_rate,
breaks = c(seq(0, 50, 5), Inf),
include.lowest = TRUE) %>%
factor(labels = paste0(">", seq(0, 50, 5))))Rather than keeping raw values (for example, on June 29, 2021, Florida had a rate of 57.77737 cases per 100,000 people), we use the cut() function to convert the values into categories: values of >0 (greater than zero), >5 (greater than five), and so on, up to a maximum value of >50 (greater than 50).
The last step is to filter the data so it includes only 2021 data (the only year depicted in Madjid’s map) and select only the variables (state, date, and incidence_rate) we’ll need to create our map. Here is the final covid_cases_rm data frame.
#> # A tibble: 18,980 × 3
#> state date incidence_rate
#> <chr> <date> <fct>
#> 1 Alabama 2021-01-01 >50
#> 2 Alabama 2021-01-02 >50
#> 3 Alabama 2021-01-03 >50
#> 4 Alabama 2021-01-04 >50
#> 5 Alabama 2021-01-05 >50
#> 6 Alabama 2021-01-06 >50
#> 7 Alabama 2021-01-07 >50
#> 8 Alabama 2021-01-08 >50
#> 9 Alabama 2021-01-09 >50
#> 10 Alabama 2021-01-10 >50
#> # ℹ 18,970 more rowsWe now have a data frame that we can combine with our geospatial data.
Adding Geospatial Data
We’ve now used two of our three data sources (COVID case data and state population data) to create the covid_cases_rm data frame we’ll need to make the map. Let’s now use the third data source: the geospatial data we saved as usa_states_geom. Simple features data allows us to merge regular data frames and geospatial data, another mark in its favor:
We merge our covid_cases_rm data frame into the geospatial data, matching the name variable from usa_states_geom to the state variable in covid_cases_rm. Next, we create a new variable called fancy_date. As the name implies, it’s a nicely formatted version of the date (for example, Jan 01 instead of 2021-01-01):
usa_states_geom_covid <- usa_states_geom %>%
left_join(covid_cases_rm, by = c("name" = "state")) %>%
mutate(fancy_date = fct_inorder(format(date, "%b. %d"))) %>%
relocate(fancy_date, .before = incidence_rate)The format() function does the formatting while the fct_inorder() function makes the fancy_date variable sort data by date (rather than, say, alphabetically, which would put August before January). Last, we use the relocate() function to put the fancy_date column next to the date column. We save this data frame as usa_states_geom_covid. Take a look at it:
#> Simple feature collection with 18615 features and 4 fields
#> Geometry type: MULTIPOLYGON
#> Dimension: XY
#> Bounding box: xmin: -2100000 ymin: -2500000 xmax: 2516374 ymax: 732103.3
#> Projected CRS: +proj=laea +lat_0=45 +lon_0=-100 +x_0=0 +y_0=0 +a=6370997 +b=6370997 +units=m +no_defs
#> First 10 features:
#> name date fancy_date incidence_rate
#> 1 Arizona 2021-01-01 Jan. 01 >50
#> 2 Arizona 2021-01-02 Jan. 02 >50
#> 3 Arizona 2021-01-03 Jan. 03 >50
#> 4 Arizona 2021-01-04 Jan. 04 >50
#> 5 Arizona 2021-01-05 Jan. 05 >50
#> 6 Arizona 2021-01-06 Jan. 06 >50
#> 7 Arizona 2021-01-07 Jan. 07 >50
#> 8 Arizona 2021-01-08 Jan. 08 >50
#> 9 Arizona 2021-01-09 Jan. 09 >50
#> 10 Arizona 2021-01-10 Jan. 10 >50
#> geometry
#> 1 MULTIPOLYGON (((-1111066 -8...
#> 2 MULTIPOLYGON (((-1111066 -8...
#> 3 MULTIPOLYGON (((-1111066 -8...
#> 4 MULTIPOLYGON (((-1111066 -8...
#> 5 MULTIPOLYGON (((-1111066 -8...
#> 6 MULTIPOLYGON (((-1111066 -8...
#> 7 MULTIPOLYGON (((-1111066 -8...
#> 8 MULTIPOLYGON (((-1111066 -8...
#> 9 MULTIPOLYGON (((-1111066 -8...
#> 10 MULTIPOLYGON (((-1111066 -8...We can see the metadata and geometry columns we discussed.
Making the Map
It took a lot of work to end up with the surprisingly simple data frame usa_states_geom_covid. And while the data may be simple, the code Madjid used to make his map is quite complex. In this section, we walk through it in pieces.
The final map is actually multiple maps, one for each day in 2021. Combining 365 days makes for a large final product, so instead of showing the code for every single day, we’ll filter the usa_states_geom_covid to show just the first six days in January:
We save the result as a data frame called usa_states_geom_covid_six_days. Here’s what this data looks like:
#> Simple feature collection with 306 features and 4 fields
#> Geometry type: MULTIPOLYGON
#> Dimension: XY
#> Bounding box: xmin: -2100000 ymin: -2500000 xmax: 2516374 ymax: 732103.3
#> Projected CRS: +proj=laea +lat_0=45 +lon_0=-100 +x_0=0 +y_0=0 +a=6370997 +b=6370997 +units=m +no_defs
#> First 10 features:
#> name date fancy_date incidence_rate
#> 1 Arizona 2021-01-01 Jan. 01 >50
#> 2 Arizona 2021-01-02 Jan. 02 >50
#> 3 Arizona 2021-01-03 Jan. 03 >50
#> 4 Arizona 2021-01-04 Jan. 04 >50
#> 5 Arizona 2021-01-05 Jan. 05 >50
#> 6 Arizona 2021-01-06 Jan. 06 >50
#> 7 Arkansas 2021-01-01 Jan. 01 >50
#> 8 Arkansas 2021-01-02 Jan. 02 >50
#> 9 Arkansas 2021-01-03 Jan. 03 >50
#> 10 Arkansas 2021-01-04 Jan. 04 >50
#> geometry
#> 1 MULTIPOLYGON (((-1111066 -8...
#> 2 MULTIPOLYGON (((-1111066 -8...
#> 3 MULTIPOLYGON (((-1111066 -8...
#> 4 MULTIPOLYGON (((-1111066 -8...
#> 5 MULTIPOLYGON (((-1111066 -8...
#> 6 MULTIPOLYGON (((-1111066 -8...
#> 7 MULTIPOLYGON (((557903.1 -1...
#> 8 MULTIPOLYGON (((557903.1 -1...
#> 9 MULTIPOLYGON (((557903.1 -1...
#> 10 MULTIPOLYGON (((557903.1 -1...Madjid’s map is giant, as it includes all 365 days. We’ll change the size of a few elements so they fit in this book.
Generating the Basic Map
Now that we have six days of data, let’s make some maps. We’ll revisit the three lines of code used to make our Wyoming maps, with some adornments to improve the quality of the visualization:
usa_states_geom_covid_six_days %>%
ggplot() +
geom_sf(
aes(fill = incidence_rate),
size = .05,
color = "grey55"
) +
facet_wrap(
vars(fancy_date),
strip.position = "bottom"
)We use geom_sf() to plot the geospatial data, modifying a couple arguments. We use size = .05 to make the state borders less prominent and color = "grey55" to set the borders to a medium gray color. Then, to make one map for each day, we use the facet_wrap() function. The vars(fancy_date) code specifies that the fancy_date variable should be used to do the faceting (in other words, make one map for each day) and strip.position = "bottom" moves the labels Jan. 01, Jan. 02, and so on to the bottom of the maps. You can see the resulting map in Figure 5.9.
Figure 5.9: A map showing the incidence rate of COVID for the first six days of 2021
Applying Data Visualization Principles to the Map
From here on out, all of the code that Abdoul Madjid uses is to improve the appearance of the maps. Many of the tweaks you will see below will feel familiar if you’ve read Chapter 3. And that’s a great benefit of making maps with ggplot: you can apply the same data visualization principles you learned when making charts to your maps as well.
The scale_fill_discrete_sequential() function from the colorspace package sets the color scale. Madjid uses the “rocket” palette (the same palette that that Cédric Scherer and Georgios Karamanis used in Chapter 3) and changes the legend title to “COVID-19 INCIDENCE RATE.” Within the guide_legend() function, Madjid puts adjusts the position and alignment as well as text properties of the title. He also puts the colored squares in one row, adjusts their height and width, and tweaks the text properties of the labels (the “>0,” “>5,” and so on).
Next, Madjid adds a title and caption using the labs() function. From there on, Madjid uses theme_minimal() (again, the same theme that Scherer and Karamanis used in Chapter 3) before making tweaks using the theme() function. These tweaks include:
- Setting the font and text color.
- Making the title and caption bold, adjusting their size, alignment, and the margins around them.
- Adjusting the size of the strip text (the Jan 01, Jan 02, and so on) and making it bold.
- Putting the legend on top of the maps and adding a bit of spacing around it.
- Removing grid lines and the longitude and latitude lines.
- Adding a bit of padding around the entire visualization and making the background a light gray.
usa_states_geom_covid_six_days %>%
ggplot() +
geom_sf(
aes(fill = incidence_rate),
size = .05,
color = "transparent"
) +
facet_wrap(
vars(fancy_date),
strip.position = "bottom"
) +
scale_fill_discrete_sequential(
palette = "Rocket",
name = "COVID-19 INCIDENCE RATE",
guide = guide_legend(
title.position = "top",
title.hjust = .5,
title.theme = element_text(
family = "Times New Roman",
size = rel(9),
margin = margin(
b = .1,
unit = "cm"
)
),
nrow = 1,
keyheight = unit(.3, "cm"),
keywidth = unit(.3, "cm"),
label.theme = element_text(
family = "Times New Roman",
size = rel(6),
margin = margin(
r = 5,
unit = "pt"
)
)
)
) +
labs(title = "2021 · A pandemic year",
caption = "Incidence rates are calculated for 100,000 people in each state.
Inspired from a graphic in the DIE ZEIT newspaper of November 18, 2021.
Data from NY Times · Tidytuesday Week-1 2022 · Abdoul ISSA BIDA.") +
theme_minimal() +
theme(
text = element_text(family = "Times New Roman",
color = "#111111"),
plot.title = element_text(
size = rel(2.5),
face = "bold",
hjust = 0.5,
margin = margin(t = .25,
b = .25,
unit = "cm")
),
plot.caption = element_text(
hjust = .5,
face = "bold",
margin = margin(t = .25,
b = .25,
unit = "cm")),
strip.text = element_text(size = rel(0.75),
face = "bold"),
legend.position = "top",
legend.box.spacing = unit(.25, "cm"),
panel.grid = element_blank(),
axis.text = element_blank(),
plot.margin = margin(t = .25,
r = .25,
b = .25,
l = .25,
unit = "cm"),
plot.background = element_rect(fill = "#e5e4e2",
color = NA)
)And there we have it: Figure 5.10 shows our recreation of Abdoul Madjid’s COVID-19 map.
Figure 5.10: Our recreation of Abdoul Madjid’s map
Making Your Own Maps
You may now be wondering: okay, great, but how do I actually make my own maps? Let’s talk about where you can find geospatial data, how to choose a projection, and how to wrangle geospatial data to get it ready for mapping.
Importing Raw Data
There are two ways to access simple features geospatial data. The first is to import raw data. Geospatial data can take a number of different formats. While ESRI shapefiles (with the .shp extension) are the most common, you might also encounter GeoJSON files (.geojson), KML files (.kml), and others. Chapter 8 of Geocomputation with R by Robin Lovelace, Jakub Nowosad, and Jannes Muenchow discusses this range of formats.
The good news for us is that a single function can read pretty much any type of geospatial data: read_sf() from the sf package. Let’s show an example of how it works. Say you’ve downloaded geospatial data about United States state boundaries from the website geojson.xyz in GeoJSON format, then saved it in the data folder as states.geojson. You can then import this data using the read_sf() function:
us_states <- read_sf(dsn = "data/states.geojson")The dsn argument (which stands for data source name) tells read_sf() where to find the file. We save the data as the object us_states.
Accessing Geospatial Data Using R Functions
You’ll sometimes have to work with raw data in this way, but not always. That’s because certain R packages provide functions for accessing geospatial data. Madjid used the usa_sf() function from the albersusa package to acquire his. Another package for accessing geospatial data related to the United States, tigris, has a number of well-named functions for different types of data. For example, we can load the tigris package and run the states() function:
We use the cb = TRUE argument to opt us out of using the most detailed shapefile and set the resolution to a more manageable 20m. Without these changes, the shapefile we’d get would be large and slow to work with. We also set progress_bar = FALSE so we won’t see the messages that tigris shares while it loads data. We then save the result as states_tigris.
The tigris package has functions to get geospatial data about counties, census tracts, roads, and more. Kyle Walker, developer of the package, wrote a book, Analyzing US Census Data: Methods, Maps, and Models in R, if you’d like to learn more about how to use it.
If you’re looking for data outside of the United States, fear not! The rnaturalearth package provides functions for importing geospatial data from across the world. For example, ne_countries() can retrieve geospatial data about various countries:
library(rnaturalearth)
africa_countries <- ne_countries(returnclass = "sf",
continent = "Africa")This code uses two arguments: returnclass = "sf" to get data in simple features format, and continent = "Africa" to get only countries on the African continent. If we save the result to an object called africa_countries, we can plot the data on a map:
Figure 5.11 shows the resulting map.
Figure 5.11: A map of Africa made with data from the rnaturalearth package
If you need geospatial data, start by looking for a package like albersusa, tigris, or rnaturalearth. If you can’t find one, fall back on using read_sf() from the sf package.
Using Appropriate Projections
Once you have access to geospatial data, you need to decide which projection to use. If you’re looking for a simple answer to this question, you’ll be disappointed. As Robin Lovelace, Jakub Nowosad, and Jannes Muenchow put it in their book Geocomputation with R, “the question of which CRS [to use] is tricky, and there is rarely a ‘right’ answer.”
If you feel overwhelmed by the task of choosing a projection, the crsuggest package, also by Kyle Walker, can give you ideas. Its suggest_top_crs() function returns a coordinate reference system that is well-suited for your data. Let’s load crsuggest and try it out on our africa_countries data:
The suggest_top_crs() function returns the projection number 28232. We can now use this value in combination with the st_transform() function in order to change the projection before we plot.
africa_countries %>%
st_transform(28232) %>%
ggplot() +
geom_sf()When run, this code generates the map in Figure 5.12.
Figure 5.12: A map of Africa made with projection number 28232
As you can see, we’ve mapped Africa with a different projection.
Bring Your Existing R Skills to Geospatial Data
The ability to merge traditional data frames with geospatial data is a huge benefit of working with simple features data. Remember that for his COVID map, Madjid analyzed traditional data frames before merging them with geospatial data. But because simple features data acts just like traditional data frames, we can just as easily apply the data-wrangling and analysis functions from tidyverse directly to a simple features object. To demonstrate this, let’s return to the africa_countries simple features data, selecting two variables (name and pop_est) to see the name and population of the countries:
The output looks like the following:
#> Simple feature collection with 51 features and 2 fields
#> Geometry type: MULTIPOLYGON
#> Dimension: XY
#> Bounding box: xmin: -17.62504 ymin: -34.81917 xmax: 51.13387 ymax: 37.34999
#> Geodetic CRS: +proj=longlat +datum=WGS84 +no_defs +ellps=WGS84 +towgs84=0,0,0
#> First 10 features:
#> name pop_est geometry
#> 1 Tanzania 53950935 MULTIPOLYGON (((33.90371 -0...
#> 2 W. Sahara 603253 MULTIPOLYGON (((-8.66559 27...
#> 11 Dem. Rep. Congo 83301151 MULTIPOLYGON (((29.34 -4.49...
#> 12 Somalia 7531386 MULTIPOLYGON (((41.58513 -1...
#> 13 Kenya 47615739 MULTIPOLYGON (((39.20222 -4...
#> 14 Sudan 37345935 MULTIPOLYGON (((24.56737 8....
#> 15 Chad 12075985 MULTIPOLYGON (((23.83766 19...
#> 25 South Africa 54841552 MULTIPOLYGON (((16.34498 -2...
#> 26 Lesotho 1958042 MULTIPOLYGON (((28.97826 -2...
#> 48 Zimbabwe 13805084 MULTIPOLYGON (((31.19141 -2...Say we want to make a map showing which African countries have populations larger than 20 million. To do so, we’d need to first calculate this value for each country. Let’s do this using the mutate() and if_else() functions, which will return TRUE if a country’s population is over 20 million and FALSE otherwise, then store the result in a variable called population_above_20_million:
africa_countries %>%
select(name, pop_est) %>%
mutate(population_above_20_million = if_else(pop_est > 20000000, TRUE, FALSE))We can then take this code and pipe it into ggplot, setting the fill aesthetic property to be equal to population_above_20_million.
africa_countries %>%
select(name, pop_est) %>%
mutate(population_above_20_million = if_else(pop_est > 20000000, TRUE, FALSE)) %>%
ggplot(aes(fill = population_above_20_million)) +
geom_sf()This code generates the map shown in Figure 5.13.
Figure 5.13: A map of Africa that highlights countries with populations above 20 million people
This is a simple example of the data wrangling and analysis you can perform on simple features data. The larger lesson is this: any skill you’ve developed for working with data in R will serve you well when working with geospatial data.
In Conclusion: R is a Map-Making Swiss Army Knife
In this short romp through the world of map-making in R, we discussed the basics of simple features geospatial data, reviewed how Abdoul Madjid applied this knowledge to make his map, discussed how to get your own geospatial data, and covered how to project it appropriately to make your own maps.
R may very well be the best tool for making maps. It’s way more flexible than Excel, way less expensive than ArcGIS, and uses syntax you already know. It also lets you use the skills you’ve developed for working with traditional data frames and the ggplot code that makes your visualizations look great. After all, Madjid isn’t a GIS expert, but he combined a basic understanding of geospatial data, fundamental R skills, and knowledge of data-visualization principles to make a beautiful map. Now it’s your turn to do the same.